光回折実験の結果、ブルー相は光の波長（数百nm）程度の格子定数の巨大な立方晶を形成していることが実証された。そうなると一つの単位格子の中に10⁷個もの分子が入っていることになる。ブルー相研究が直面した最大の問題は、これほどの多数の分子が格子中でどのような配列構造を形成しているか、であった。その配列の基本形態は「ねじれ（twist）」である。ここで、そのねじれが織りなす分子配列構造について紹介する。

　キラルネマチック相は図１のように分子配列にらせん構造を有している。このような構造は自然界に多く見られ、代表的な分子組織構造のひとつである。らせん構造を形成する液晶相は一般にキラル分子から構成されている（あるいはキラル分子を含んでいる）。キラル分子同士の分子間相互作用により、棒状の液晶分子がその長軸を互いに平行に配列させるより少しねじれた状態の方が安定となり、そのねじれる向きが全ての分子間で同じであることがらせん構造の形成の原因と理解されている。この場合、分子配列のねじれは、分子ラテラル方向（長軸に垂直方向）の一つの軸に沿って形成される、いわゆる単純ねじれ（simple twist）である。ところが、分子1個に着目すると、分子は長軸周りに高速で回転しており、分子間相互作用は全ラテラル方向に等方的に作用するはずである。したがって、ラテラル方向に隣接する全ての分子に対してねじれ配列を誘起するはずである。単純ねじれでは、ねじれを誘起しない方向ができてしまう。

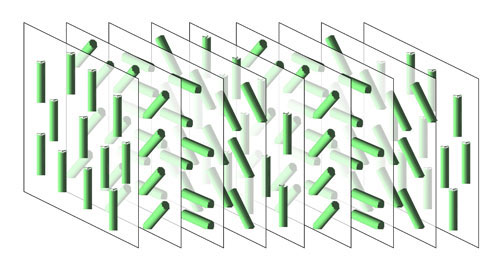
図１キラルネマチック相における分子のらせん配列

では、なぜキラルネマチック相は単純ねじれをとるか？図２を見ていただきたい。いまx軸上に棒状分子を長軸がｘ軸に平行になるように並べる（分子長軸に沿ってはねじれ配列はない）。x軸上のA地点から分子をy軸に沿ってねじれながら配列させる。Aからx軸上のある程度離れたB地点からも同様にy軸に沿ってねじれ配列させる。ねじれが90度になったところで今度はx軸に沿って両方向から互いに出会うように配列させる。ここで、ねじれはy軸に沿ってのみ形成される単純ねじれを適用すると、分子はx軸に沿ってはねじれずに向きをそろえたまま配列するので、A、Bの両方向からきた分子の向きは図２(a)のように一致する（向きを変える地点でのねじれが90度以外でもこれは成立する）。ところが、y軸だけではなくx軸に沿ってもねじれを形成させると図２(b)のように出会った地点で向きが合わなくなる（A、Bの距離がちょうどねじれの半ピッチの場合を除けば）。これらの操作を全空間で行うと何が言えるか？単純ねじれを適用させると、ある地点での分子の向きが決まると任意の位置の分子の向きは配列操作のルートに依らず決定でき、全空間の分子の向きが規定できる。すなわち、分子を三次元空間に連続的に配置できることになる。ところが、二軸に対してねじれを形成させると。ある地点での分子の向きが決まっても、別の地点の向きは図２(b)のように配列させるルートに依存して異なることになる。すなわち、二軸方向のねじれを全空間に適用すると、必ず分子の向きが不連続になる欠陥が生じることになる。この欠陥の発生を避け連続体になろうとするトポロジー的な要請がキラル液晶がねじれ配列を一軸のみに自発的に限定する理由である。

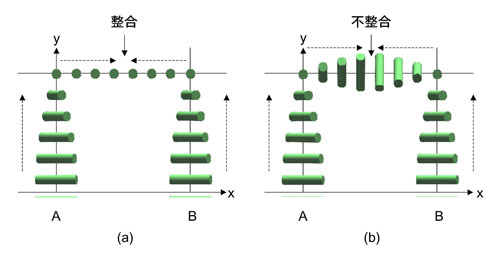
図２ねじれ配列におけるフラストレーション。(a)単純ねじれの場合、任意の距離離れたA, Bからの配列操作で不整合は生じない。(b)二重ねじれの場合、不整合が生じる。

　ところが、単純ねじれでは本来あるねじれ軸以外の方向のねじれ力が抑圧されることになる。では、このねじれ力が大きくなると何が起こるか？分子の全てのラテラル方向にねじれを誘起させると図３(b)のような配列になる。この配列は二重ねじれ（double twist）と呼ばれている。完全な二重ねじれは中心の分子とその周囲のみで、半径方向に広がるにつれ二重ねじれは薄まる。中央付近の分子は、全てのラテラル方向のねじれが許容されているという点で単純ねじれよりも安定である。この安定領域のみで形成される高次構造体が、図４に示す二重ねじれシリンダーである。二重ねじれは広域に拡張すると欠陥が生じるため、二重ねじれシリンダーは空間を連続で埋める基本構造にはなり得ないのは上述の通りである。ところがブルー相、はその不整合をもったままで二重ねじれシリンダーを基本構造としているのである。

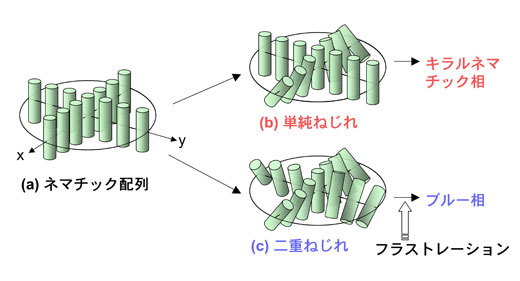
図３単純ねじれと二重ねじれの比較。

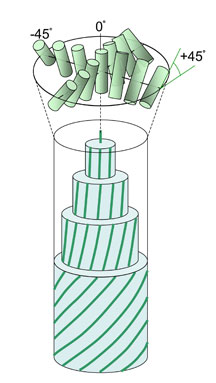
図4二重ねじれシリンダー内の分子配列の模式図。